Machine Learning Engineer (Ads) Interview Questions
A Guide to Pass the MLE interview.
1 梯度不稳定
1.1 概念
在深度神经网络中的梯度是不稳定的,在靠近输入层的隐藏层中或会消失,或会爆炸。这种不稳定性才是深度神经网络中基于梯度学习的根本问题。
1.2 根本原因
前面层上的梯度是来自后面层上梯度的乘积。当存在过多的层时,就会出现梯度不稳定场景,比如梯度消失和梯度爆炸。
划重点:梯度消失和梯度爆炸属于梯度不稳定的范畴
2 梯度消失与梯度爆炸
2.1 概念
梯度消失:在神经网络中,当前面隐藏层的学习速率低于后面隐藏层的学习速率,即随着隐藏层数目的增加,分类准确率反而下降了。这种现象叫梯度消失。
梯度爆炸:在神经网络中,当前面隐藏层的学习速率低于后面隐藏层的学习速率,即随着隐藏层数目的增加,分类准确率反而下降了。这种现象叫梯度爆炸。
其实梯度消失和梯度爆炸是一回事,只是表现的形式,以及产生的原因不一样。
2.2 产生原因
梯度消失:(1)隐藏层的层数过多;(2)采用了不合适的激活函数(更容易产生梯度消失,但是也有可能产生梯度爆炸)
梯度爆炸:(1)隐藏层的层数过多;(2)权重的初始化值过大
隐藏层的层数过多
从深层网络角度来讲,不同的层学习的速度差异很大,表现为网络中靠近输出的层学习的情况很好,靠近输入的层学习的很慢,有时甚至训练了很久,前几层的权值和刚开始随机初始化的值差不多。因此,梯度消失、爆炸,其根本原因在于反向传播训练法则,属于先天不足。具体见下图:
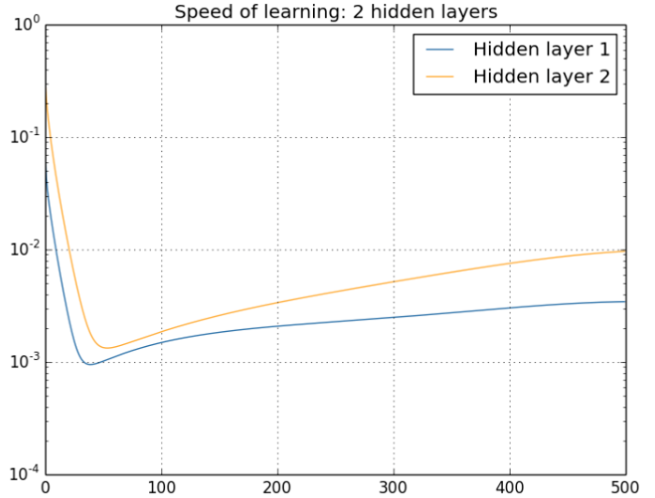
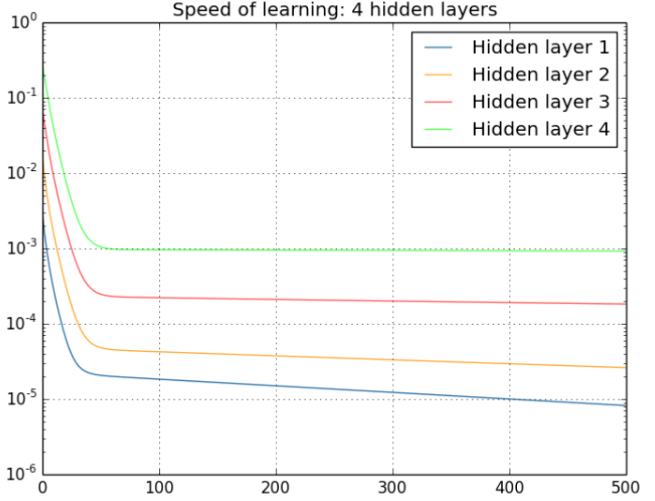
从上图可以非常容易的看出来:对于四个隐层的网络来说,第四隐藏层比第一隐藏层的更新速度慢了两个数量级!!!
激活函数
我们以下图的反向传播为例,假设每一层只有一个神经元且对于每一层都可以用公式1表示,其中σ为sigmoid函数,C表示的是代价函数,前一层的输出和后一层的输入关系如公式1所示。我们可以推导出公式2。

σ为sigmoid函数,其导数的图像如下图所示:
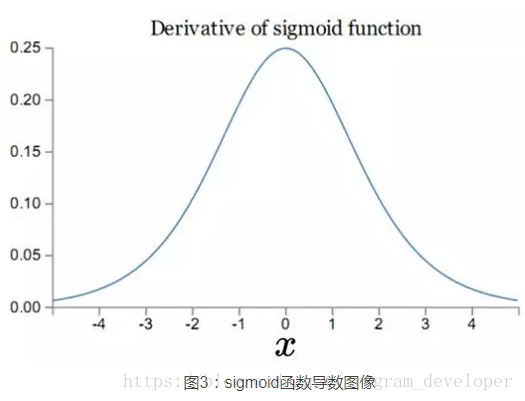
可见,\(\sigma^{'}(x)\) 的最大值为 \(1/4\) ,而我们一般会使用标准方法来初始化网络权重,即使用一个均值为0标准差为1的高斯分布。因此,初始化的网络权值通常都小于1,从而有 \(|\sigma^{'}(z)w|<1/4\) 。对于2式的链式求导,层数越多,求导结果越小,最终导致梯度消失的情况出现。所以说,sigmoid函数一般不适合用于神经网络中,那神经网络中应该用哪些激活函数呢?等等就为你揭晓!
2.3 初始化权重的值过大
当 \(|\sigma^{'}w|>1\) , 也就是w比较大的情况下,根据2式的链式相乘可得(反向传播),则前面的网络层比后面的网络层梯度变化更快,引起了梯度爆炸的问题。所以,在一般的神经网络中,权重的初始化一般都利用高斯分布(正态分布)随机产生权重值。
3 解决梯度消失和爆炸的方法
梯度消失和梯度爆炸问题都是因为网络太深,网络权值更新不稳定造成的,本质上是因为梯度反向传播中的连乘效应。对于更普遍的梯度消失问题,可以考虑一下几种方案解决:
3.1 预训练加微调
3.2 梯度裁剪
3.3 使用合理的参数初始化方案,如He初始化
3.4 用ReLU、Leaky-ReLU、P-ReLU、R-ReLU、Maxout等替代sigmoid函数。
具体见这里
3.5 Batch Normalization
具体见这里
基本思想
问题
网络输入x随着网络深度加深,分布逐渐发生偏移,往非线性函数的取值区间的上下限两端靠近(对于Sigmoid函数来说,意味着激活输入值WU+B是大的负值或正值),所以这导致后向传播时低层神经网络的梯度消失,这是神经网络收敛慢的本质原因。
方法
BN就是通过一定的规范化手段,把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的正态分布,使得激活输入值落在非线性函数对输入比较敏感的区域,这样输入的小变化就会导致损失函数的大变化,从而梯度变大,避免梯度消失问题产生,而且梯度变大意味着学习收敛速度快,能大大加快训练速度。
例子
假设没有经过BN调整前x的原先正态分布均值是-6,方差是1,那么意味着95%的值落在了[-8,-4]之间,那么对应的Sigmoid(x)函数的值明显接近于0,这是典型的梯度饱和区,在这个区域里梯度变化很慢,为什么是梯度饱和区?请看下sigmoid(x)如果取值接近0或者接近于1的时候对应导数函数取值,接近于0,意味着梯度变化很小甚至消失。而假设经过BN后,均值是0,方差是1,那么意味着95%的x值落在了[-2,2]区间内,很明显这一段是sigmoid(x)函数接近于线性变换的区域,意味着x的小变化会导致非线性函数值较大的变化,也即是梯度变化较大,对应导数函数图中明显大于0的区域,就是梯度非饱和区。
经过BN后,目前大部分Activation的值落入非线性函数的线性区内,其对应的导数远离导数饱和区,这样来加速训练收敛过程。
如果都通过BN,那么不就跟把非线性函数替换成线性函数效果相同了?但多层线性网络跟一层线性网络是等价的。这意味着网络的表达能力下降了,深度的意义就没有了。
所以BN为了保证非线性的获得,对变换后的满足均值为0方差为1的x又进行了scale加上shift操作(y=scale*x+shift),每个神经元增加了两个参数scale和shift参数,这两个参数是通过训练学习到的,意思是通过scale和shift把这个值从标准正态分布左移或者由移一点并长胖一点或者变瘦一点,每个实例挪动的程度不一样,这样等价于非线性函数的值从正中心周围的线性区往非线性区动了动。核心思想应该是想找到一个线性和非线性的较好平衡点,既能享受非线性的较强表达能力的好处,又避免太靠非线性区两头使得网络收敛速度太慢。
3.6 引入门控机制
3.7 残差连接(Residual Connections)
skip connection 跨越隐藏层链接。
3.8 Dense Connections
中间层相互连接。连得越多,梯度问题就越复杂,越稳定。